ne_q1spCompilingGui

A program that acts as a frontend for compiling q1 maps.  Lets you set your compiler tools and settings and then does it all for you.

Requirements:

most likely this requires vb .net runtimes 2.0 which is easily gettable from microsoft yet very annoying to install. sorry, but that’s what comes from using visual basic to make stuff.

[Download] (v1.03)

Instructions:

My creatively named “ne_q1spCompilingGui” is a sometimes useful GUI. essentially, it acts as a graphical batch file that will copy files for you, run qbsp, vis and light with whatever settings you want and easily let you toggle command line arguments on and off.

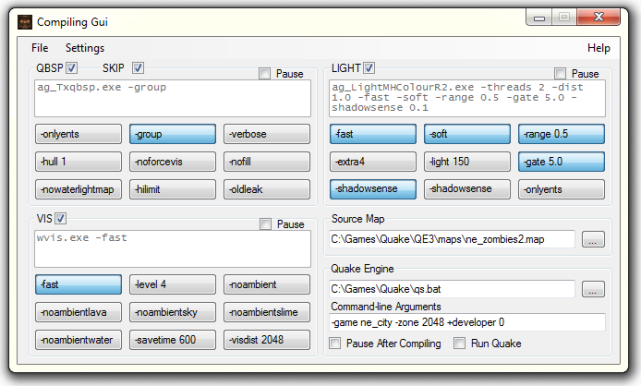
here’s the main window:

you’ll first want to set up your compilers.
open the Settings menu and select Folder Setup (it’s the only menu item there…)
that will bring up the Preferences window:

• first select the folder where all your compilers are located.

• second, enter the compiler filenames in the appropriate spots. the command-line argument text boxes are for arguments that are always used (for example -altaxis, or the arguments i use for aguirre’s light utility shown above)

• third, if you are using gtkr1.4 (or another editor that requires map format converting), select the “Map must be converted before compiling?” checkbox.

this will expand the area and let you specify the map converter (in the image, it is aguirre’s convmap). command-line arguments are self explanatory, whatever you need to use to convert your map.

• fourth, you’ll have to specify a working folder. you don’t actually have to, but i highly recommend it. if you don’t want to use a working folder, just use the same folder as your tools folder or your output folder. it’s messy, but that’s your choice. :P

a working folder is used to compile in. the .map file will be copied there from wherever you saved it out of your map editor. the .bsp file will be copied out of there into the output folder (which is selected underneath).

this means that your .wad files should be either in the working folder itself, or a subfolder. a “wad”

this is nice because it gives you a limited form of backup.

• the output folder is your /maps folder, essentially. it’s where the .bsp file goes after it’s compiled. if a .bsp file is already present there, the newly compiled version will overwrite it.

• once you’re finished, click on done.

this brings you back to the main window.

the check box on the left controls whether the compiler will be run or not. useful for turning off vis if you’re running a -onlyents update, or turning off qbsp and light if you want to re-vis your map.

the ‘Pause’ checkbox will tell the command prompt to pause with a ‘Press any key to continue’ after the compiler is finished.

the buttons underneath each represent a command-line argument.

you can easily create your own by simply right-clicking in the empty space below the text boxes and selecting ‘Add’. (you can also edit already existing buttons by right-clicking on them and selecting ‘Edit’, or you can delete any you don’t want anymore by selecting ‘Remove’). You can add up to 9 and you can combine multiple arguments into the same button if you always plan to use the same ones.

you can toggle any of those command line arguments on and off just by clicking on them.

the text box give you a quick preview of each compiler command-line.

you can see that the command line arguments that were specified in the preference window are always present, and can’t be toggled off.

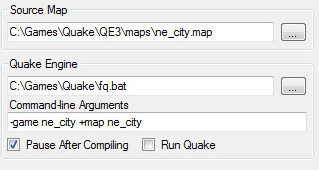
once you’re happy with your settings, pick the map you want to compile by clicking the “…” button in the ‘Source Map’ section.

do the same to select your quake engine, and then type in whatever command-line arguments you want to send to the engine.

you can tell the program to pause after all compilers have run as well as make it automatically start quake once it’s finished.

now, all that’s left it to open the File menu and select Compile (or press Ctrl+C). if you did not check the “Run Quake” check box, you can run quake manually with File->Run Quake or by pressing Ctrl+R.

finally, all settings are saved when you quit the program in config.ini (in the same folder that this program is in). it’s in text format but not really readable. i’d recommend not modifying it yourself as it can cause the program to crash

that about covers anything you need to know to use this thing.